Inteligencia Artificial aplicada a Ciencia de Materiales. Parte 2: Los bandgaps

Resumen: Esta entrada tiene como propósito principal informar sobre diversas estrategias implementadas en la caracterización de materiales cristalinos para el desarrollo de modelos de aprendizaje de máquina que estimen la brecha energética entre bandas (mejor conocida como bandgap, por su nombre en inglés). En general, quienes han desarrollado estos modelos de aprendizaje de máquina tienen como objetivo que éstos reproduzcan los valores obtenidos de cálculos tipo DFT, que hacen uso de funcionales PBE, GLLB, o HSE, o del método de cuasipartículas G₀W₀. Lo anterior, con el fin de abaratar costos de cómputo y sondear nuevos compuestos posibles de manera más eficiente. La caracterización seguida por diversos autores se realiza mediante rasgos (o descriptores) que sólo consideran la composición química del material, así como mediante incorporación de rasgos que describen la estructura del material. Estos rasgos provienen tanto de la literatura como de cálculos químico cuánticos implementados por los autores de las publicaciones revisadas. Algunos de estos métodos de caracterización tienen como último fin la predicción de múltiples propiedades de los materiales, tales como las implementadas en Magpie, SchNet, SOAP, u OFM. Hasta ahora, y considerando diversos algoritmos de aprendizaje de máquina como diferentes tamaños de conjuntos destinados al entrenamiento de éstos, el error absoluto promedio que se puede obtener es de algunas décimas de electron-volts.

Introducción

La brecha energética entre bandas, también conocida como banda prohibida, es la propiedad que determina el grado de carácter metálico de un material cristalino. Aquellos compuestos con una brecha energética diferente a cero son esencialmente no metales, los cuales se consideran como semiconductores o aislantes, según la magnitud de esta brecha. Además, la brecha energética determina el área de aplicaciones que un material cristalino puede tener. Por ejemplo, para aplicaciones en celdas solares, los materiales deben tener una brecha energética cercana a límite de Queisser – Schockly (1.3 – 1.7 eV). Cuando el material ha sido sintetizado, la brecha energética suele determinarse mediante espectroscopía UV – visible o espectroscopía de rayos X. Por otra parte, el cálculo de la magnitud de estas brechas energéticas in silico suele hacerse mediante teoría de funcionales de la densidad (DFT), siendo el funcional PBE (Perdew-Burke-Ernzerhof) el más concurrido. Aunque con este funcional de gradiente generalizado (GGA) se obtienen resultados razonables sobre parámetros de estructura de un material, este funcional suele subestimar la magnitud de la brecha energética. Otros métodos implementados para el cálculo de brechas energéticas hacen uso del funcional GLLB (Gritsenko-Leeuwen-Lenthe-Baerends), del potencial mBJ (Becke-Johnson modificado), del funcional híbrido HSE (Heyd-Scuseria-Ernzerhof), o el método de cuasipartículas G₀W₀, que hace uso de la función de Green G y un potencial de apantallamiento W. No obstante, el costo computacional de estos métodos se incrementa en este orden. Por esta razón, diversos autores han implementado métodos de aprendizaje de máquina a fin de a) reproducir las brechas energéticas, ya sea calculadas o determinadas experimentalmente, y b) estimar las brechas energéticas de estos materiales con estos métodos a un menor costo computacional. Además del algoritmo de aprendizaje de máquina y del conjunto de datos utilizado en su entrenamiento, la caracterización de las muestras (materiales cristalinos) de ese conjunto de datos influye en el desempeño del modelo que se desarrolle. Esto último, revisar cómo diversos autores han concebido los rasgos (o descriptores) es el propósito de este manuscrito.

En la primera parte de esta revisión se resume la caracterización implementada en modelos de aprendizaje de máquina de tipo extremo a extremo (conocidas en inglés como end-to-end), que buscan la predicción de múltiples propiedades de materiales sin importar la composición o estructura de estos. Entre estas plataformas destacan SchNet, Magpie, OFM, CGCNN, MEGNET, y ATCNN. En esta revisión, omitimos la explicación de la caracterización mediante kernels de traslapes suaves de posiciones atómicas, SOAP (del inglés smooth overlap of atomic positions) y referiremos al lector a los artículos originales (Bartok et. al., 2013, y De et. al. 2016). En la segunda parte de esta revisión se resumen los trabajos relevantes que existen sobre esta área.

1. Métodos de caracterización general para la predicción de propiedades de materiales

1.1 Magpie

Magpie es el acrónimo en inglés de Materials Agnostic Platform for Informatics and Exploration. Esta plataforma sirvió para calcular los rasgos utilizados en la caracterización de materiales implementada por Logan Ward y colaboradores (2016). La caracterización de estos materiales se hizo mediante de un vector de 145 rasgos. Estos rasgos sólo consideran la composición del material, y pueden clasificarse como rasgos estequiométricos (6 en total), rasgos de estructura electrónica (4), rasgos de compuestos iónicos (3), y rasgos sobre la estadística de las propiedades de los elementos de la tabla periódica (115). Los rasgos estequiométricos corresponden a la norma L^p, con p = 0, 2, 3, 5 y 7, del vector de fracciones atómicas de los elementos constitutivos del material. Los rasgos de estructura electrónica corresponden a las fracciones ponderadas de ocupación de los orbitales de valencia según sea de tipo s, p, d, o f. Los rasgos iónicos describen a) la posibilidad de que el compuesto sea de tipo iónico, b) el carácter iónico del compuesto, en el caso hipotético de que se tratara de un compuesto binario formado por el par de elementos con mayor diferencia de electronegatividad, y c) el carácter iónico promedio del compuesto. Los rasgos sobre estadística de los elementos toman en cuenta los valores mínimos, máximos, promedio ponderado, desviación promedio y moda de 23 propiedades de los elementos presentes en la fórmula. La lista de estos rasgos se puede consultar fácilmente en el material suplementario de la publicación de Ward y colaboradores (2016). Esta caracterización fue implementada de manera parcial anteriormente por B. Meredig y colaboradores en 2014.

Ward y coautores utilizaron 228,676 compuestos de la base de datos OQMD (del inglés Open Quantum Materials Database) a fin de reproducir las brechas energéticas de estos materiales mediante regresión lineal y árboles de decisión sujetos a poda. Los compuestos utilizados por los autores que correspondieron a aquellos de menor energía para una misma composición. Utilizando una validación cruzada en bloques de 10 (k-fold cross validation), el error absoluto promedio (MAE) reportado por ellos fue de 0.202 eV, mediante regresión lineal, y 0.070 eV, con árboles de decisión sujetos a poda. Finalmente, los autores utilizaron los modelos desarrollados para determinar la brecha energética de algunos compuestos reportados por Meredig et. al. como no sintetizados. Los autores presentan algunas composiciones como Mn₆CCl₈ y VCu₅Cl₉ como candidatos a ser usados en celdas solares.

1. 2 DTNN y SchNet

DTNN fue publicada por Kristof T. Schütt y colaboradores en 2017 para calcular la energía total de una molécula a partir de la suma de las energías individuales de sus átomos.  Las moléculas son caracterizadas mediante a) un vector c_i, cuyas componentes están asociadas a las cargas nucleares de sus átomos y b) una matriz de distancias interatómicas D, la cual modela la interacción entre átomos. Estas distancias interatómicas son expandidas mediante bases de tipo gaussiano, para tomar en cuenta diferentes tipos de interacción.  Es importante señalar que las componentes del vector asociado a las cargas nucleares de los átomos son inicializadas de manera aleatoria. Por esta razón, las componentes de dicho vector son refinadas mediante una serie de iteraciones, donde las distancias interatómicas asociadas al átomo i juegan un papel importante en la actualización de dichas componentes. Al término de este refinamiento, el vector asociado a las cargas nucleares del átomo se alimenta a una red neuronal de tipo perceptrón multicapas, la cual determina la contribución a la energía total de la molécula en cuestión. Los autores de DTNN suponen que después de cada iteración en el refinamiento, los átomos de la molécula son encasillados en sus propios ambientes químicos. La precisión que los autores obtuvieron con DTNN fue de 1 kcal/mol, utilizando compuestos orgánicos de la base de datos GBD. Otro de los alcances que demostró tener esta caracterización de los compuestos fue su capacidad para determinar los potenciales químicos asociados a diferentes partes de una molécula.

Con DTNN, las interacciones son modeladas mediante capas de tensores, es decir, rasgos de átomos y distancias interatómicas se combinan mediante parámetros tensoriales. En 2018, Schütt y colaboradores publicaron una variante de DTNN que llamaron SchNet. SchNet modela las interacciones usando convoluciones de filtro continuo con redes generadoras de filtro. Con SchNet, los autores determinaron propiedades de moléculas orgánicas de la base de datos QM9 (131 mil moléculas orgánicas con hasta nueve átomos pesados) como el HOMO, LUMO, brecha energética, energía interna (a temperatura ambiente y 0K), energía libre de Gibbs con un error absoluto promedio de algunas decenas de meV (0.063 eV, para el caso específico de la brecha energética)

1. 3 OFM

Tien Lam Pham y colaboradores publicaron en 2017 un método para caracterizar a los materiales con base en la distribución de los electrones de la capa de valencia de sus átomos. Los autores denominaron a esta caracterización de los materiales como matriz de campo orbital, OMF (acrónimo en inglés de orbital field matrix). La clave del método desarrollado por Pham y colaboradores está en representar la configuración electrónica de la capa de valencia como un vector de ceros y unos (one-hot vector), donde 1 representa cierta cantidad de electrones llenando a un determinado orbital de valencia. Por ejemplo, considerando un vector de 32 componentes, donde cada componente representa a una cantidad de electrones en los orbitales de valencia:

{s¹, s², p¹, …, p⁶, d¹, …, d¹⁰, f¹, …, f¹⁴}

la configuración de los electrones de valencia del átomo de cloro ([Ne] 3s²3p⁵) se representa como un vector con componentes igual a uno en las posiciones asociadas a s² y p⁵ (segunda y séptima componente), mientras que el resto se llena de ceros. De manera similar, para un átomo de sodio ([Ne]3s¹), su representación vectorial tiene como único elemento diferente de cero a la primera posición.

A continuación, y siguiendo la ley de empaquetamiento de Pauling que establece que los átomos no metálicos (cloro en nuestro ejemplo) rodean a los metálicos (sodio), se obtiene una matriz de 32×32 tomando en cuenta el producto entre el vector del metal (como vector columna) y al del no metal (vector reglón). Los elementos de la matriz resultante se modifican por una corrección que toma en cuenta a) la contribución al número de coordinación del átomo no metálico vecino, y b) la distancia entre el átomo central y vecino, que se representa como una función de tipo 1/r_ij. Para evaluar la contribución al número de coordinación del átomo central los autores utilizaron la librería de Python pymatgen, que se basa en lo publicado por M. A. O’Keeffe (1979) sobre poliedros de Voronoi y que permite tratar con geometrías de baja simetría.

El procedimiento anterior, de obtener las matrices y corregirlas, se efectúa para todos los átomos metálicos que están en la primera esfera de coordinación. Las matrices obtenidas posteriormente se suman para obtener finalmente la matriz de campo orbital del sistema, la cual sirve para ser alimentada a algún algoritmo de aprendizaje de máquina.

Pham y colaboradores concibieron la representación OFM para determinar momentos magnéticos locales de aleaciones binarias entre metales de transición y lantánidos (652 compuestos), así como para determinar las energías de formación de estas aleaciones y las de las moléculas de la base de datos QM7. Los resultados obtenidos por ellos tuvieron un error absoluto promedio de 0.05 µ_B, 0.112 eV (aleaciones metálicas) y 0.027 (moléculas orgánicas). El cuadrado del coeficiente de correlación menor obtenido fue de 0.93.

1.4 CGCNN

CGCNN es el acrónimo en inglés de redes neuronales convolucionales de grafos de cristales (Crystal-graph convolutional neural network), y es un método propuesto por Xie & Grossman en 2018. Este método se mencionó al final de la Parte 1 de esta revisión, y retoma la caracterización implementada por Isayev et. al. (2017) en Fragmentos de materiales etiquetados con propiedades (Property-Labelled Materials Fragments, PLMF) para construir rasgos de átomos (i-nodos), v_i^(t), y de enlaces (i,j-aristas), u_(i,j), de un grafo cristalino. Estos grafos cristalinos representan a la celda unitaria de un cristal. Además, los átomos (nodos) están relacionados a los diferentes ambientes atómicos presentes en el mismo cristal. La CGCNN desarrollada por Xie & Grossman demostró ser eficiente en la estimación de energías de formación, energías de Fermi, razón de Poisson, módulos de bulk y de corte, así como en brechas energéticas, en donde se obtuvo un MAE = 0.388 eV. Este resultado en brechas energética se obtuvo al utilizar 16548 materiales del repositorio Materials Project.

El método CGCNN tiene reminiscencias de DTNN y SchNet, en el sentido de que los rasgos de átomos son refinados mediante convoluciones que utilizan los rasgos de átomos de una capa anterior y los rasgos de enlace. La regla de actualización de estos rasgos de átomos es:

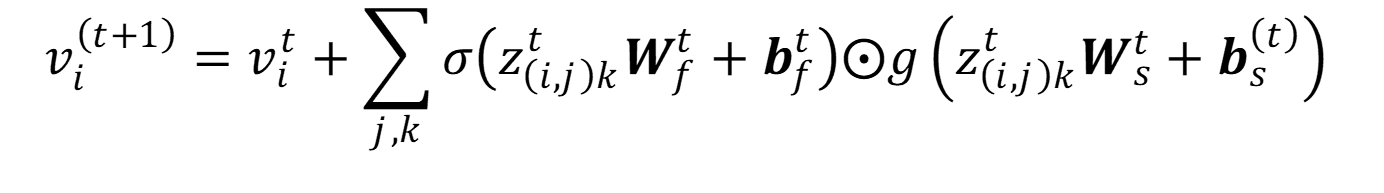
En la ecuación anterior, t cuenta cada una de las convoluciones de CGCNN (t = 0 representa los datos de entrada de la red), W y b son parámetros propios de la red convolucional sujetos a optimización. En la ecuación, σ representa la función sigmoide, g a una función de activación, y z_(i,j)k es un vector que se obtiene de la concatenación de los rasgos de los átomos i y j conectados a través del k-ésimo enlace que los une.

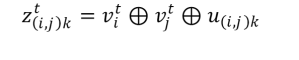
El lector puede notar que u_(i,j) es el mismo vector sin importar de que etapa del proceso de convoluciones se trate.

Todos los vectores obtenidos en cada una de las t-convoluciones, para cada uno de los i-vectores de los átomos que constituyen al grafo cristalino, son sumados después de haber sido sujetos a la función softmax:

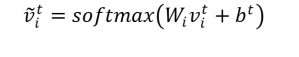
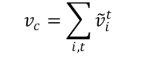
v_c se denomina vector del grafo cristalino y sirve de dato de entrada a una red de tipo perceptrón multicapa, la cual sirve para determinar las propiedades comentadas antes.

1. 5 MEGNET

Chi Chen y colaboradores (2019) desarrollaron su propia plataforma de aprendizaje de máquina para la predicción de propiedades de materiales, la cual tiene por nombre MEGNet (acrónimo de MatErials Graph Network, redes de grafos de materiales). Como su nombre lo indica, la plataforma utiliza conceptos de la teoría de grafos, tales como vértice y arista, para diseñar los rasgos que caracterizan a los materiales, sean éstos moleculares o cristalinos. En concreto, los autores utilizan la propuesta de redes de grafos publicada por Peter W. Battaglia y coautores. Entre los rasgos para describir los vértices (átomos del material) se encuentra el número atómico, la quiralidad, la hibridización, la aromaticidad, por ejemplo. Estos rasgos son vectores de tipo one-hot y variables binarias. Los rasgos utilizados de tipo arista describen a los enlaces existentes entre los átomos (tipo de enlace, formación de anillos) y a las distancias entre los átomos mediadas por funciones de tipo gaussianas con un radio de corte. Además, los autores utilizan variables del sistema, tales como el promedio del número atómico o enlaces por átomo, así como las variables termodinámicas temperatura, presión (como variable de tipo binaria) y entropía (variable de tipo binaria), para describir la energía interna, entalpía y energía de formación de Gibbs.  Los datos de entrada son alimentados a redes neuronales de tipo perceptrón multicapa de diferente profundidad. Los autores utilizaron tanto el banco de datos de moléculas orgánicas QM9, publicado por Faber y colaboradores, así como la base de datos de Materials Project, para utilizar energías de formación y brechas energéticas de compuestos cristalinos. El error absoluto promedio en la estimación de brechas energéticas fue de 0.33 +/- 0.01 eV.

1. 6 ATCNN

Shuming Zeng y colaboradores (2019) publicaron su método para determinar propiedades de materiales utilizando, lo que ellos mismos han llamado, redes neuronales convolucionales de tablas atómicas, ATCNN (acrónimo del inglés atom table convolutional neural network). Las propiedades que estudiaron Zeng y colaboradores fueron la temperatura crítica de transición superconductora, la energía de formación, y la brecha energética. Los autores obtuvieron la información de las bases de datos SuperCon y OQMD, así como de la literatura. En concreto, los autores dispusieron de 3896 y 5886 materiales para mapear las tablas atómicas a brechas energéticas y energías de formación, así como de 13,598 materiales superconductores. Las tablas atómicas propuestas por Zeng y sus colaboradores son esencialmente matrices de 10×10, donde cada elemento de matriz corresponde a la fracción atómica de cada elemento presente en la fórmula química del material. Esta caracterización da lugar a representar las fracciones atómicas de hasta 120 elementos químicos (diez elementos de la tabla periódica por renglón). La matriz obtenida sirve como dato de entrada de una red neuronal convolucional, la cual extrae por sí misma los rasgos relevantes para la estimación de las propiedades de los materiales. Esta caracterización, por lo tanto, también sólo toma en consideración la composición de un material. La justificación que dan los autores está en que, experimentalmente, existe una correspondencia única y determinada entre la estructura que adopta y su composición, de manera que la composición está entrelazada con la estructura cristalina. Zeng y colaboradores obtuvieron errores absolutos promedio de 0.307 eV en la estimación de brechas energéticas. Estrategias similares para caracterizar a los materiales con base únicamente en su composición química han sido publicadas por Dipendra Jha. et. al. (2018), Rhys E. A. Goodall et. al. (2020), y Yashaswi Pathak et. al. (2020). Este último utilizó autoencoders variacionales condicionados para desarrollar un generador de materiales con base en restricciones sobre la entalpía de formación, energía por átomo y volumen por átomo. La caracterización seguida por Pathak y colaboradores se basa en vectores de dimensión once de tipo one-hot. Estos vectores representan a cada uno de los primeros 89 elementos de la tabla periódica. La dimensión de estos vectores está asociada al subíndice de ese elemento en la fórmula (entero), que toma un valor entero entre 0 y 10.

2. Trabajos publicados

Ghanshyam Pilania y colaboradores (2016) utilizaron regresión Ridge de kernels (KRR, acrónimo de Kernel Ridge Regression) para determinar la brecha energética, obtenida con el funcional GLLB optimizado a sólidos, de óxidos de perovskitas dobles. Este funcional es utilizado también para corregir la subestimación que normalmente se obtiene de cálculos DFT que involucran funcionales de tipo GGA o LDA. Los autores tomaron los datos de 1306 perovskitas dobles de la base de datos CMR (acrónimo de Computational Materials Repository). Parte de la caracterización que implementan Pilania y colaboradores depende de la fórmula de estos compuestos de perovskitas doble, la cual se representa como AA’BB’O₆. En la fórmula, los elementos A y A’ ocupan un sitio con una misma geometría (dodecaédrica). Lo mismo ocurre con B y B’ (octaédrica). La caracterización de los compuestos empieza considerando siete rasgos de cada elemento A, A’, B, B’ de la fórmula, que son la electronegatividad de Pauling (χ), el potencial de ionización (I), la energía de los niveles más bajo (l) y más alto (h) ocupados, y los radios de los orbitales s, p, y d de valencia. Algunos de estos rasgos se tomaron de la literatura, mientras que otros se obtuvieron de cálculos con el funcional PBE. A continuación, se calcularon los valores absolutos de la suma y la diferencia de rasgos por parejas AA’ y BB’, es decir, se calculan | χ_A + χ_A’ |, | χ_A – χ_A’ |, | χ_B + χ_B’ |, | χ_B – χ_B’ |, | I_A + I_A’ |, | I_A – I_A’ |, | I_B + I_B’ |, | I_B – I_B’ |, etc. Según se haya utilizado la suma o la diferencia, estos rasgos se representan como χ_A⁺ o χ_A^–, por ejemplo, para el caso de las electronegatividades de los átomos A y A’. La intención de los autores de calcular estas diferencias y sumas en obtener rasgos que reflejen los dos tipos de redes de poliedros A y B que subyacen dentro de la estructura de perovskita doble.

Los autores denominaron a este conjunto de 28 rasgos simetrizados rasgos primarios. Esto se debe a que ellos además jugaron con las funciones x, x^1/2, x², x³, In(1+x), y exp(x), donde x es un rasgo primario. El resultado de estas funciones fue objeto de multiplicaciones de pares y tercias de estos rasgos, con lo cual Pilania et. al obtuvieron 1’229,312 rasgos que denominaron rasgos compuestos. Desde luego, los autores no utilizaron el más de un millón de rasgos compuestos, sino que tomaron los 40 más relevantes para la estimación de la brecha energética mediante un modelo de operador de selección y contracción mínima absoluta (LASSO, del inglés least absolute shrinkage and selection operator). Por último, los autores seleccionaron los 16 mejores rasgos primarios, y 16 mejores rasgos compuestos, después de obtener la correlación de Pearson. La lista de los rasgos finales utilizados por Pilania y colaboradores se puede consultar en el material suplementario que acompaña a su publicación. La menor raíz del error cuadrático que reportan, en los compuestos escogidos para el test, fue de 0.36 eV.

Joohwi Lee y colaboradores (2016) utilizaron regresión lineal y máquinas de vectores soportados para mapear las brechas energéticas obtenidas con los funcionales de densidad PBE y mBJ a la brecha energética obtenida con el método G₀W₀. Además, los autores utilizaron otros descriptores para establecer esos mapeos, tales como la valencia, el número atómico, la electronegatividad, entre otras propiedades que tienen que ver con los elementos. Ellos reportaron raíces del error cuadrático promedio (RMSE, por su acrónimo en inglés) que van de 0.59 eV, cuando utilizan un solo descriptor, que corresponde al resultado obtenido vía PBE o mBJ, a 0.24 eV, cuando utilizaron más descriptores y mediante máquinas de vectores soportados.

Los autores utilizaron 270 compuestos inorgánicos cristalinos, binarios y ternarios, y que correspondieron a estructuras de tipo wurtzita, cloruro de cesio, blenda o halita. Los compuestos utilizados por Lee et. al. no contuvieron metales de transición en su fórmula, y se trató de compuestos con menos de 25 átomos en su celda unitaria. Además, estos compuestos eran de brecha directa e indirecta.

Por otra parte, Arunkumar C. Rajan et. al. (2018), desarrollaron un clasificador binario de materiales bidimensionales con fórmula MX, con una precisión del 94 % en la clasificación entre metales y semiconductores. Posteriormente, los autores utilizaron su clasificador para seleccionar algunos compuestos semiconductores de tipo MX y establecer un mapeo entre las propiedades de dichos materiales, calculadas vía DFT, con su brecha energética obtenida utilizando el método GW. Rajan y colaboradores reportaron obtener un RMSE = 0.14 eV.

Ya Zhou y colaboradores (2018) utilizaron máquinas de vectores soportados para correlacionar la brecha energética experimental de 3896 materiales con sólo propiedades de los elementos de los materiales. Los autores justificaron usar únicamente rasgos composicionales debido a que muchas veces falta información cristalográfica de los materiales reportados en la literatura. En total, los autores emplearon 136 rasgos, los cuales se obtienen de 34 propiedades diferentes tras utilizar la adición, diferencia, el valor mínimo y el valor máximo de éstos. Entre las propiedades utilizadas estuvieron información de la tabla periódica, diferentes tipos de radio y electronegatividades, potenciales de ionización, cantidad de electrones en los orbitales, temperaturas de fusión y ebullición, calores de fusión y evaporación. Las brechas energéticas utilizadas por Zhou et. al. fueron medidas por reflectancia difusa, resistividad, espectroscopía UV-visible, fotoconductividad y fotovoltaje de superficie. Los autores obtuvieron RMSE = 0.45 (R² = 0.90) en la estimación de brechas energéticas, y una precisión del 92 % en la clasificación de los materiales entre las clases metal y no metal.

Wissam A. Saidi y colaboradores (2020) utilizaron redes neuronales convolucionales para estimar la brecha energética, obtenida con el método GLLBC + SOC, de halogenuros de compuestos ABX₃ con estructura tipo perovskita cúbica, donde B: Pb o Sn, X: Cl, Br, I, y A era un catión poliatómico (varios de ellos, orgánicos). Los autores utilizaron en total un conjunto de 862 compuestos diferentes, los cuales fueron caracterizados a través de 11 rasgos: los radios de los iones A, B y X, las primeras y segundas energías de ionización del catión A, la energía de formación del compuesto, el volumen del par AX, la brecha energética calculada vía otros cálculos DFT, el parámetro de red, el momento dipolar de la molécula orgánica y el ángulo octaédrico. Los rasgos calculados vía DFT se obtuvieron utilizando el funcional PBEsol. Algo novedoso de la estrategia adoptada por Saidi y colaboradores, lo cual se justifica en la pequeña cantidad de compuestos en el conjunto utilizado, es que primero implementaron una red convolucional que clasifica a los compuestos en seis intervalos de brecha energética. Posteriormente, se implementa una red convolucional que establece la regresión entre los datos de entrada y la brecha energética experimental.  De esta manera, los autores obtienen un error promedio de 0.14 eV (no se dice si es un error absoluto o la raíz del error cuadrático).  Esta manera de estratificar los algoritmos de aprendizaje de máquina también fue reportada por Ward et. al. (2016). No obstante, los autores concluyen que su estudio subestima la importancia del diseño meticuloso en el uso de aprendizaje de máquina que contribuya a las relaciones estructura-propiedades de los halogenuros metálicos con estructura tipo perovskita.

L. Weston y C. Stampfl (2018) utilizaron regresión de vectores soportados y cálculos DFT para explorar nuevos compuestos, con fórmula I₂ – II – IV – VI₄, que adopten la estructura tipo kesterita para aplicaciones fotovoltaicas. Este tipo de estructura se deriva de la blenda de zinc. Los autores diseñaron 1568 compuestos considerando a todos los elementos de las familias I, II, IV y VI, de la tabla periódica, además de algunos otros pertenecientes a los metales de transición. De este conjunto, sólo utilizaron 200 compuestos para calcular la brecha energética con el funcional HSE06. Tras los cálculos, los autores obtuvieron 184 brechas energéticas debido a que los cálculos de 16 compuestos I₂ – II – IV – VI₄ no convergieron. Estas brechas energéticas sirvieron para implementar la regresión de vectores soportados. Para el mapeo de las brechas energéticas, los autores caracterizaron a los compuestos con un vector de 12 rasgos: la electronegatividad, el radio iónico, y el periodo al que pertenece cada elemento de la fórmula I₂ – II – IV – VI₄. Estos rasgos fueron suficientes para obtener un RMSE = 0.283 eV, con R² = 0.957, utilizando una estrategia de validación cruzada en bloques de 10. Adicionalmente, los autores desarrollaron un clasificador binario utilizando regresión logística, a fin de diferenciar a los compuestos entre de brecha directa (78) o de brecha indirecta (108). Utilizando la caracterización implementada en la regresión, Weston & Stampfl obtuvieron una precisión (accuracy, no confundir con precision) de 73 % en la clasificación. No obstante, tras una expansión polinomial de segundo orden del vector de dimensión 12, lo autores consiguieron incrementar la precisión del clasificador hasta 89 %. La lista de los rasgos utilizados en esta expansión puede consultarse en el material suplementario de la publicación de Weston & Stampfl. Finalmente, los autores utilizaron el regresor desarrollado para estimar las brechas energéticas de los compuestos restantes. Aquellos compuestos con una brecha estimada entre 1.2 y 1.8 eV fueron sujetos a validación mediante cálculos con el funcional HSE. La lista de estos compuestos I₂ – II – IV – VI₄ de estructura kesterita, con potencial aplicación fotovoltaica, se puede consultar en la publicación mencionada.

Kamal Choudhary y colaboradores (2018) utilizaron árboles de decisión con potenciación del gradiente para explorar nuevos compuestos bidimensionales. Para esto, los autores utilizaron la base de datos JARVIS-DFT, publicada por ellos en 2017, que contenía en aquel entonces 24,549 energías de formación; brechas energéticas de 22,404 y 10,954 obtenidas con los funcionales OptB88vdW y TBmBJ, respectivamente; 10,954 módulos de volumen y de corte, así como 616 energías de exfoliación de materiales bidimensionales. Los materiales fueron caracterizados con rasgos estructurales como funciones de distribución radial, distribución de vecinos cercanos, distribuciones de ángulos entre enlaces y ángulos diedros, y rasgos inspirados en los métodos de campo de fuerza COMB (acrónimo de charge-optimized many-body), ReaxFF (del inglés reaction-force field), y AMBER (acrónimo de assisted model building with energy refinement). Estos rasgos fueron sujetos de otras operaciones como suma, diferencia, producto y cociente, para obtener nuevos rasgos químicos. La caracterización implementada da lugar a un vector de 1557 rasgos. Estos rasgos se pueden consultar en el material suplementario al artículo publicado por Choudhary et. al. (2018). Los autores obtuvieron un MAE = 0.32 eV y MAE = 0.44 eV en el mapeo de brechas energéticas obtenidas vía OptB88vdW y TBmBJ, respectivamente. Choudhary et. al. utilizaron posteriormente su modelo de aprendizaje de máquina desarrollado en compuestos reportados anteriormente como candidatos a ser bidimensionales y semiconductores. Los autores seleccionaron aquellos materiales bidimensionales semiconductores evaluados con a) una energía de formación negativa, b) brecha energética (mBJ) entre 1.2 – 3 eV, y c) energía de exfoliación menor a 200 meV, para ser validados mediante cálculos DFT. Algunos compuestos validados fueron CuI, Mo₂O₅, y InS.

Xing-Yu Ma y coautores (2019) utilizaron diversos algoritmos de aprendizaje de máquina para eficientemente sondear el espacio químico de posibles compuestos bidimensionales (2D) de oxihalogenuros octaédricos, OOH (acrónimo en inglés de octahedral oxyhalides). Los autores calcularon vía DFT la brecha energética de 300 compuestos 2D-OOHs. Estos 300 compuestos fueron escogidos aleatoriamente de 5300 con fórmula A₂B₂X₂, donde B: O, S, Se o Te; y X se trataba de algún halógeno. Estos compuestos tenían una estructura de simetría ortorrómbica. Los rasgos más importantes en la caracterización de los compuestos 2D-OOH, encontrados tras implementar análisis de componentes principales (PCA, por su acrónimo en inglés), fueron aquellos relacionados con el factor octaédrico. En concreto, los autores utilizaron ocho factores octaédricos modificados a fin de describir la distorsión de la geometría octaédrica entorno al átomo A. Estos rasgos son similares a los cocientes de sumas de radios atómicos utilizados por Gómez-Peralta et. al. (2020, 2021) para la clasificación de compuestos cristalinos. Otros rasgos empleados por Ma y sus colaboradores fueron potenciales de ionización, afinidades electrónicas, electronegatividades en la escala Martynov-Batsanov, cargas iónicas, número de electrones de valencia, de los átomos de los compuestos A₂B₂X₂. En total, los autores partieron de 52 rasgos iniciales, mismos que se reducen a 26 tras excluir rasgos redundantes. Con esta caracterización de los compuestos 2D-OOH A₂B₂X₂, se obtienen errores cuadráticos promedios de al menos 0.086 y con R² = 0.835, mediante el uso de regresión con potenciación del gradiente (GBR, acrónimo en inglés de gradient boosting regression).Con este modelo de aprendizaje de máquina desarrollado, Ma y colaboradores estimaron la brecha energética de los 5300 compuestos restantes del espacio de 2D-OOH. Posteriomente, los autores escogieron aquellos compuestos con una brecha energética entre 0.9 – 1.6 eV, de baja toxicidad y costo, para calcular sus propiedades electrónicas mediante teoría de perturbaciones de funcionales de la densidad. Los autores sugirieron los compuestos Bi₂Se₂Br₂, Bi₂Se₂BrI, y Bi₂Se₂I₂ como candidatos potenciales para aplicaciones optoelectrónicas por sus altos coeficientes de absorción en el espectro visible.

Bart Olsthoorn y colaboradores publicaron en 2019 una actualización de la base de datos de materiales orgánicos (OMDB, por su acrónimo en inglés), que anteriormente habían publicado Stanislav S. Borysov y coautores en 2017. Los compuestos orgánicos fueron tomados de Crystallography Open Database, los cuales se reportaron en las revistas Organometallics, Organic Letters, Journal of Organic Chemistry, y Organic & Biomolecular Chemistry. La base de datos OMDB contiene 12,500 compuestos orgánicos cristalinos. Las fórmulas de estos compuestos orgánicos abarcan 65 elementos de la tabla periódica, siendo uranio el más pesado de todos ellos. Además, estos compuestos abarcan 69 grupos espaciales, todos los sistemas cristalinos, y en promedio hay 82 átomos dentro de la celda unitaria de estos materiales, siendo 7 y 208 la menor y mayor cantidad de átomos por celda unitaria. Las brechas energéticas de los compuestos de la base de datos OMDB se calcularon vía DFT, utilizando el funcional PBE. En el artículo publicado por Olsthoorn et. al. se informa que la brecha energética promedio de los compuestos orgánicos de OMDB es de 3.05 eV, con desviación estándar de 1.03 eV. La distribución de estas brechas energéticas sigue un perfil de Wigner-Dyson,

con α = 4.61, β = 0.28, y x corresponde al valor de la brecha energética.

Olsthoorn et. al. entrenaron modelos de aprendizaje de máquina que estimaron la brecha energética de estos compuestos orgánicos utilizando 1) regresión Ridge de kernels mediante la caracterización de los compuestos por SOAP, 2) y SchNet. Tras el entrenamiento de estos modelos, los autores reportaron un MAE en el conjunto de compuestos orgánicos destinado a prueba de 0.430 y 0.415 eV con SOAP y SchNet, respectivamente. Además, Olsthoorn et. al. estimaron que se necesita aproximadamente 267 millones de compuestos orgánicos para conseguir un MAE en el conjunto de prueba de 0.1 eV. Finalmente, los autores usaron los modelos desarrollados para estimar la brecha energética de 260 092 compuestos orgánicos disponibles de COD, los cuales tuvieron como máximo 500 átomos por celda unitaria. Olsthoorn et. al. encontraron 3343 compuestos orgánicos cristalinos candidatos a ser usados en celdas solares, considerando el límite Schockley-Weisser.

Recientemente, Ricardo Espinosa y colaboradores (2022) utilizaron los compuestos de la base de datos publicada por Olsthoorn et. al. para determinar sus brechas energéticas, mediante redes neuronales convolucionales, a partir de una caracterización basada en imágenes tridimensionales de las moléculas de estos compuestos. Los autores reportaron un MAE = 0.678 eV utilizando esta caracterización. Posteriormente, Espinosa y colaboradores modificaron la estructura de 10 compuestos de la OMDB a fin de probar la red convolucional desarrollada. Las brechas energéticas de estos compuestos modificados se validaron a través de cálculos DFT, tras los cuales obtuvieron un MAE = 0.4371 eV entre dichos cálculos químico cuánticos y los predichos por la red convolucional.

Ekaterina I. Marchenko y colaboradores (2020) utilizaron el método SOAP para determinar las brechas energéticas de compuestos de perovskitas híbridas bidimensionales (A’)_2/qA_n-1B_nX_3n+1. En la fórmula, [A’]^q+ representa a un catión orgánico de carga q = 1+ o 2+, el cual funge como espaciador entre conjuntos de n-capas con estructura tipo perovskita. Los autores utilizaron los compuestos de su propia base de datos, que se puede consultar en www.pdb.nmse-lab.ru. El MAE obtenido por los autores fue de 0.103 eV, utilizando 515 compuestos de perovskitas híbridas dimensionales. Marchenko et. al. reportaron además que su modelo de aprendizaje de máquina reproducía la tendencia que hay entre un número de capas de perovskita híbrida creciente y la brecha energética decreciente de estos materiales.

Andrew S. Rosen y colaboradores (2020) publicaron la base de datos QMOF (acrónimo de Quantum MOF), la cual contiene propiedades calculadas por métodos químico cuánticos de más de 14,000 estructuras metalórganicas, mejor conocidas como MOFs (del inglés Metal Organic Framework). Los MOFs se tomaron tanto del Cambridge Structural Database (CSD) como de Computation-Ready, Experimental (CoRE) MOF database. Para la curación de los MOFs, los autores tomaron en cuenta que los materiales que formaran parte de QMOF tuvieran al menos un átomo de carbono, que sus estructuras estuvieran libres de disolvente, que el principio de electroneutralidad se cumpliera, y que la distancia interatómica fuera mayor a 0.74 Å. Las propiedades de estos MOFs fueron calculadas con el funcional PBE, incorporando correcciones por dispersión de tipo D3(BJ).  La brecha energética de los MOFs calculados va de 0 – 6.45 eV. La distribución de estas brechas energéticas tuvo un perfil de dos gaussianas, con máximos en 0.9 eV (3,544 MOFs) y en 2.9 eV (12,169 MOFs). Estos máximos se atribuyen a que los materiales son de capa cerrada y de capa abierta, respectivamente. En la base de datos QMOF se tiene presencia de todos los metales de la tabla periódica, excepto de Hf, Ta, Os, Pm, Ac, Pa, Po, At, Fr, Ra, así como de todos los elementos posteriores al Am. Los metales que más abundaron fueron Cu, Zn, Cd y Ag, los cuales están presentes en 2882, 2665, 2538 y 1213 MOFs. Además de las brechas energéticas, en la base de datos QMOF se dispone de otras informaciones tales como el tipo de brecha, las energías en los bordes de las bandas de valencia y de conducción, así como la polarización de espín de estas bandas. Rosen et. al. implementaron regresión Ridge de kernels a fin de mapear los MOFs, con sus estructuras tal como fueron reportados experimentalmente (sin optimizar computacionalmente), a las brechas energéticas obtenidas por los cálculos DFT PBE-D3(BJ). Para la caracterización, los autores utilizaron la matriz de Coulomb de seno, las redes convolucionales de grafos de cristal (CGCNN), la matriz de campo orbital, y SOAP. Con la matriz de Coloumb de seno (Faber et. al. 2015, que abordamos en la entrada anterior), y con CGCNN, se obtuvieron errores absolutos promedios de 0.529 y 0.274 eV. Este error fue de 0.42 eV, con la matriz de campo orbital, y de 0.357 eV, utilizando SOAP. Finalmente, los autores utilizaron el modelo desarrollado mediante CGCNN para determinar la brecha energética de algunos MOFs que no fueron incorporados a QMOF, a fin de encontrar compuestos aptos para aplicaciones de celdas solares, los cuales posteriormente fueron validados con cálculos DFT utilizando el funcional HSE06.

Comentarios finales

En esta revisión se puso énfasis en la caracterización de materiales para la construcción de los datos de entrada, obviando la parte que concierne a las fortalezas e inconvenientes de los métodos de aprendizaje de máquina usados por diversos autores, así como del tamaño del conjunto de muestras empleado. Los métodos de aprendizaje de máquina desarrollados constituyen funciones que mapean los rasgos basados en la composición y/o la estructura de un material a la brecha energética entre bandas y que, por lo tanto, pueden ser sujetos a métodos de optimización para la búsqueda de nuevos materiales a un menor costo computacional.

Hemos visto que métodos que sólo toman en cuenta la composición del material, con un error absoluto promedio menor a 0.30 eV. No obstante, estos métodos están restringidos a considerar un sólo tipo de estructura cristalina, o a la estructura termodinámicamente más estable entre todas las que un mismo material puede adoptar. Sobre esta última consideración, las composiciones de materiales candidatos a aplicaciones de celdas solares podrían despertar suspicacia sobre las condiciones termodinámicas a las que estos materiales pueden ser sintetizados o bajo las cuales tendrían operar. En este sentido, la incorporación de rasgos con información estructural sobre ambientes locales resulta de mucha utilidad para desarrollar modelos de aprendizaje de máquina con propuestas aún más razonables sobre nuevos compuestos. Estos rasgos estructurales están diseñados de manera que consideran la inmutabilidad del material cristalino ante diversas operaciones de simetría.

Todos los desarrollos de aprendizaje de máquina aplicados a estimar brechas energéticas han transcurrido en un plazo menor a 8 años, por lo que todavía hay camino por recorrer en el desarrollo de modelos dependientes en temperatura y presión, para lo cual se necesitarán toneladas de datos al respecto.

Agradecimientos Al Consejo Nacional de Ciencia y Tecnología (CONACyT), por la beca posdoctoral otorgada (CVU: 620161). Sin ese apoyo no tendría el tiempo ni los recursos para sentarme a revisar y elaborar esta entrada.

Referencias

1. M. A. O’Keeffe “A proposed rigorous definition of coordination number” Acta Cryst. A 35, 772-775 (1979)
2. A. P. Bartok, R. Kondor, G. Csanyi “On representing chemical environments” Physical Review B87, 184115 (2013)
3. B. Meredig, A. Agrawal, S. Kirklin, J. E. Saal, J. W. Doak, A. Thompson, K. Zhang, A. Choudhary, C. Wolverton “Combinatorial screening for new materials in unconstrained composition space with machine learning” Physicial Review B 89, 094104 (2014)
4. F. Faber, A. Lindmaa, O. A. von Lilienfeld, R. Armiento “Crystal structure representations for machine learning models of formation energies” International Journal of Quantum Chemistry 115, 1094-1101 (2015)  
5. S. De, A. P. Bartok, G. Csanyi, M. Ceriotti “Comparing molecules and solids across structural and alchemical space” Physical Chemistry Chemical Physics 18, 13754-13769 (2016)
6. J. Lee, A. Seko, K. Shitara,K. Nakayama, I. Tanaka “Prediction model of bandgap for inorganic compounds by combination of density functional theory calculations and machine learning techniques”. Physical Review B 93, 115104 (2016)
7. G. Pilania, A. Mannodi-Kanakkithodi, D. Uberuaga, R. Ramprasad, J. E. Gubernatis, T. Lookman “Machine learning bandgaps of double perovskites” Scientific Reports 6, 19375 (2016)
8. L. Ward, A. Agrawal, A. Choudhary, C. Wolverton “A general-purpose machine learning framework for predicting properties of inorganic materials” npj Computational Materials 2, 16028 (2016)
9. S. S. Borysov, R. M. Geilhufe, A. V. Balatsky “Organic materials database: An open-acces online database for data mining” PLos ONE 12, e0171501 (2017)
10. O. Isayev, C. Oses, C. Toher, E. Gossett, S. Curtarolo, A. Tropsha, Nature Comm. 2017, 8, 15679
11. T. L. Pham, H. Kino, K. Terakura, T. Miyake, K. Tsuda, I. Takigawa, H. C. Dam “Machine learning reveals orbital field interaction in materials” Science and Technology of Advanced Materials, 18, 756-765 (2017)
12. K. T. Schütt, F. Arbabzadah, S. Chmiela, K. R. Müller, A. Tkatchenko “Quantum-chemical insights from deep tensor neural networks” Nature Communications 8, 13890 (2017)
13. P. W. Battaglia, J. B. Hamrick, V. Bapst, A. Sanchez-Gonzalez, et. al. “Relational inductive biases, deep learning and graph networks” arXiv:1806.01261 (2018)
14. K. Choudhary, B. DeCost, F. Tavazza “Machine learning with force field-inspired descriptors for materials: fast screening and mapping energy landscape» Physical Review Materials 2, 083801 (2018)
15. T. Xie, J. Grossman “Crystal graph convolutional neural network for an accurate and interpretable prediction of material properties” Physical Review Letters 120, 145301 (2018)
16. D. Jha, L. Ward, A. Paul, W.K. Liao, A. Choudhary, C. Wolverton, A. Agrawal “ElemNet: Deep learning the chemistry of materials from only elemental composition” Scientific Reports 8, 17593 (2018)
17. A. C. Rajan, A. Mishra, S. Satsangi. R. Vaish, H. Mizuseki, K.-R. Lee, A. K. Singh “Machine-learning-assisted accurate band gap predictions of functionalized MXene” Chemistry of Materials 30, 4031 – 4038 (2018)
18. K. T. Schütt, H. E. Sauceda, P. J. Kindermans, A. Tkatchenko, K. R. Müller “SchNet: A deep learning architecture for molecules and materials” Journal of Chemical Physics 148, 241730 (2018)
19. L. Weston, C. Stampfl, “Machine learning the band gap properties of kesterite I2 – II – IV – VI quaternary compounds for photovoltaics applications” Physical Review Materials 2, 085407 (2018)
20. Y. Zhou, A. M. Tehrani, J. Brgoch “Predicting the band gap of inorganic solids by machine learning” Journal of Physical Chemistry Letters 9, 1668-1673 (2018)
21. C. Chen, W. Ye, Y. Zhuo, C. Zheng, S. P. Ong “Graph Networks as a Universal Machine Learning Framework for Molecules and Crystals” Chemistry of Materials 31, 3564-3572 (2019)
22. X. Y. Ma, J. P. Lewis, Q. B. Yan, G. Su “Accelerated discovery of two-dimensional optoelectronic octahedral oxyhalides via high-throughput ab-initio calculations and machine learning” Journal of Physical Chemistry Letters 10, 6734-6740 (2019)
23. B. Olsthoorn, R. M. Geilhufe, S. S. Borysov, A. V. Balatsky “Band gap prediction for large organic crystal structures with machine learning” Advanced Quantum Technologies 2, 1900023 (2019)
24. S. Zeng, Y. Zhao, G. Li, R. Wang, X. Wang, J. Ni “Atom table convolutional neural networks for an accurate prediction of compounds properties” npj Computational Materials 5, 84 (2019)
25. J. I. Gómez-Peralta, X. Bokhimi “Discovering new perovskites with artificial intelligence” Journal of Solid State Chemistry 285, 121253, (2020)
26. R. E. A. Goodall, A. A. Lee “Predicting materials properties without crystal structure: deep representation learning from stoichiometry” Nature Communications 11, 6280 (2020)
27. E. I. Marchenko, S. A. Fateev, A. A. Petrov, V. V. Korolev, A. Mitrofanov, A. V. Petrov, E. A. Goodilin, A. B. Tarasov “Database of two-dimensional hybrid perovskite materials: Open access collection of crystal structures, band gaps, and atomic partial charges predicted by machine learning” Chemistry of Materials 32, 7383-7388 (2020)
28. Y. Pathak, K. S. Juneja, G. Varma, M. Ehara, U. D. Priyakumar “Deep learning enabled inorganic material generator” Physical Chemistry Chemical Physics 22, 26935-26943 (2020)
29. W. A. Saidi, W. Shadid, E. Castelli “Machine-Learning structural and electronic properties of metal halide perovskites using a hierarchical convolutional neural network” npj Computational Materials 6, 36 (2020)
30. J. I. Gómez-Peralta, N. G. García-Peña, X. Bokhimi “Crystal-site-based artificial neural networks for material classification” Crystals 11, 1039 (2021)
31. A. S. Rosen, S. M. Iyer, D. Ray, Z. Yao, A. Aspuru-Guzik, L. Galiardi, J. M. Notestein, R. Q. Snurr “Machine learning the quantum-chemical properties of metal-organic frameworks for accelerated materials discovery” Matter 4, 1578-1597 (2021)
32. R. Espinosa, H. Ponce, J. Ortiz-Mena “A 3D ortogonal visión-based band-gap prediction using deep learning: A proof of concept” Computational Materials Science 202, 110967 (2022)

Bases de Datos

1. a) OQMD: https://oqmd.org/ (Consultado el 08/03/2022); b) Saal, J. E., Kirklin, S., Aykol, M., Meredig, B., and Wolverton, C. «Materials Design and Discovery with High-Throughput Density Functional Theory: The Open Quantum Materials Database (OQMD)», JOM 65, 1501-1509 (2013), c) Kirklin, S., Saal, J.E., Meredig, B., Thompson, A., Doak, J.W., Aykol, M., Rühl, S. and Wolverton, C. «The Open Quantum Materials Database (OQMD): assessing the accuracy of DFT formation energies», npj Computational Materials 1, 15010 (2015)
2. GBD a) Blum, L. C. & Reymond, J.-L. “970 million druglike small molecules for virtual
   screening in the chemical universe database gdb-13” J. Am. Chem. Soc. 131,
   8732, (2009); b) Reymond, J.-L. “The chemical space project” Acc. Chem. Res. 48, 722–730
   (2015)
3. QM7: R. Ramakrishnan, P. O. Dral, M. Rupp, O. A. von Lilienfeld “Quantum chemistry structures and properties of 134 kilo molecules” Sci. Data. 1, 140022 (2014)
4. QM9: M. Rupp, A. Tkatchenko, K. R. Müller, O. A. von Lilienfeld “Fast and accurate modeling of molecular atomization energies with Machine Learning” Phys. Rev. Lett. 108, 058301 (2012)
5. SuperCon: https://dice.nims.go.jp/news/2021/12/20211221.html (Consultado el 08/03/2022)
6. CMR: https://cmr.fysik.dtu.dk/ (Consultado el 08/03/2022)
7. JARVIS-DFT: K. Choudhary, I. Kalish, R. Beams, F. Tavazza “High -throughput identification and characterization of two-dimensional materials using density functional theory” Sci. Rep. 7, 5179 (2017)
8. Materials Project: https://materialsproject.org (Consultado el 08/03/2022)

Lecturas complementarias sobre cálculos químico cuánticos

1. Sobre el método GW: F. Bechstedt, F. Fuchs, G. Kresse “Ab-initio theory of semiconductor band structures: new developments and progress” Physica Status Solidi B 246, 1877-1892 (2009)
2. DFT en estado sólido: R. J. Hasnip, K. Refson, M. I. J. Probert, J. R. Yates, S. J. Clark, C. J. Pickard “Density functional theory in the solid state” Philosophical Transactions of the Royal Society A 372, 20130270 (2014)
3. DFT en general: P. Verma & D. G. Truhlar “Status and challenges of density functional theory” Trends in Chemistry 2, 302-318 (2020)