Inteligencia Artificial aplicada a Ciencia de Materiales. Parte I

Desde hace meses he tenido ganas de escribir un Review sobre los trabajos que existen de aplicación de algoritmos de Inteligencia Artificial en Ciencia de Materiales y, aún más, hacerlo en castellano. Por diferentes razones he venido postergando su escritura. Este tiempo, en el que me he mantenido fuera, me ha servido para tomar la decisión de hacer esta revisión en partes y a través de este blog, y no mediante la publicación en una revista indizada. Sobre esto último, próximamente quiero compartir con ustedes estos motivos, que espero den lugar a una discusión sobre el proceso de producción científica, cuyo átomo es la publicación en editoriales hegemónicos. Entre estas razones está que en esta época el acceso a la información se puede hacer casi inmediata, sin las trabas que las editoriales suelen poner de seis u ocho meses que comprenden la aprobación por el editor, el proceso de revisión entre pares, la modificación del manuscrito y su publicación. No subestimo la revisión entre pares, pero considero que en esta época las editoriales sólo ralentizan este proceso, además de que esa revisión y retroalimentación se hace mejor si se publica a través de este tipo de espacios, que potencialmente pueden captar un mayor número de pares.

Y para comenzar con esta revisión, me tomaré la libertad de compartir con ustedes un fragmento de mi tesis doctoral, aprobada en diciembre de 2020 y defendida hace ya casi un año, en la que hago una pequeña revisión sobre estos trabajos.

**************************************************************************************************************

Después de la introducción anterior sobre IA, aprendizaje de máquinas y redes neuronales, merece la pena revisar algunos problemas que se han abordado en el campo de la química, la física y la ciencia de materiales. La aplicación del aprendizaje de máquina en el área científica ha sido, sobre todo, en problemas de aprendizaje supervisado. Parte de la justificación de revisar los problemas abordados en ciencia tiene que ver con que una caracterización adecuada de los datos de entrada de las muestras influirá en el éxito de cualquier algoritmo de aprendizaje de máquina, como es el caso de las redes neuronales. Las redes neuronales son una herramienta que dota de autonomía a un programa de computadora en la búsqueda de correlación entre datos.

Lorenz, Behler y Artrith ^{[41 – 43]} han utilizado las energías obtenidas de cálculos con teoría de funcionales de la densidad a fin de crear una red neuronal que reconstruya la superficie de energía potencial (PES, por su acrónimo en inglés). En los sistemas en donde se ha probado este enfoque con redes neuronales es en la disociación de moléculas diatómicas sobre superficies metálicas y en las fases anatasa, brookita y rutilo del óxido de titanio (IV).  La caracterización del sistema de partículas se basa en la construcción de funciones de simetría radial G_i¹ y angular G_i² de cada átomo.

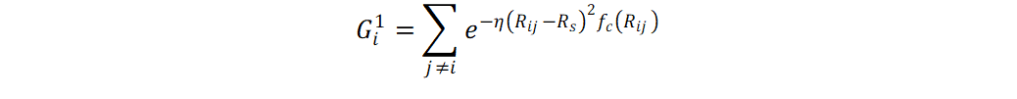
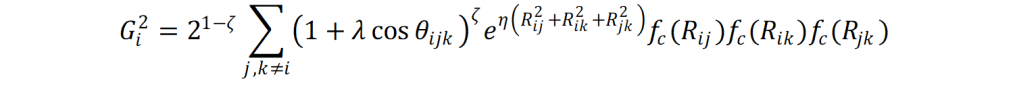
En las ecuaciones anteriores, η, R_s , ζ,  son parámetros que se ajustan y que deben ser encontrados para cada sistema. Por otro lado, f_c define una función de corte con radio R_c = 6 Å:

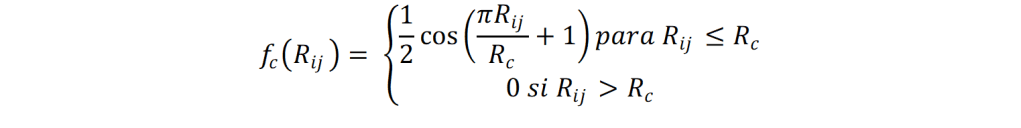
Los datos de entrada son alimentados a una red neuronal para cada átomo. Los nodos de salida de cada red neuronal por átomo se conectan a una última red neuronal que es la que calcula la energía del sistema de partículas. El error cuadrático promedio en la energía que se obtiene con este tipo de redes neuronales es del orden de 5 – 6 meV (0.12 – 0.14 kcal/mol). En adición, una de las ventajas que se tienen al usar redes neuronales es que el tiempo de cómputo depende de la cantidad de átomos.

Hansen et. al. ^[44] han utilizado diversos algoritmos de aprendizaje de máquina, entre ellos los perceptrones multicapa, para determinar las energías de atomización de moléculas con hasta 23 átomos. La colección de muestras utilizada por Hansen et. al. constó de 7165 moléculas de átomos de los dos primeros periodos de la tabla periódica. La caracterización de las moléculas se consiguió a través de la matriz de Coulomb. La matriz de Coulomb ^[45] (Rupp, 2012) de un compuesto se define como:

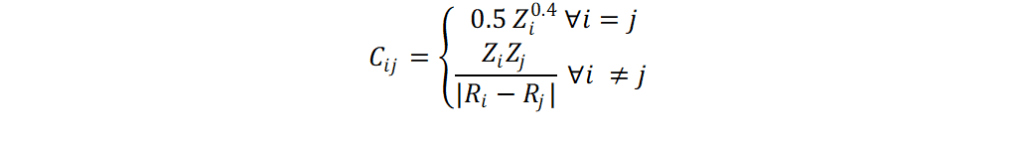
Con la matriz de Coulomb se obtiene una representación en dos dimensiones de una estructura tridimensional, como lo es una molécula. Z_i y R_i designan la carga nuclear y la coordenada atómica del átomo i. La caracterización de una molécula a través de la matriz de Coulomb tiene dos fuertes desventajas: moléculas con diferente cantidad de átomos dan lugar a diferentes tamaños de matriz, y que no existe una manera concreta de ordenar los átomos a lo largo de las filas y columnas de una matriz. El primer problema se resuelve homogenizando el tamaño de la matriz mediante la adición de columnas y filas con valores nulos (padding). Para el segundo problema, Hansen et. al. utilizaron tres enfoques diferentes: 1) la obtención de los valores propios de la matriz; 2) El ordenamiento en forma decreciente de los valores C_ij a lo largo de las filas y columnas; y 3) La construcción de un tensor en el que se apilan diferentes matrices de Coloumb del mismo sistema. La diferencia entre las matrices de un mismo tensor está en la permutación del orden entre columnas y filas. El mejor error cuadrático promedio obtenido por Hansen et. al., utilizando Perceptrones multicapa, fue de 5.96 kcal mol^-1. Este resultado se obtuvo mediante la caracterización por tensores de mil matrices de Coulomb apiladas.

La caracterización de las muestras de una colección que se deriva de la matriz de Coulomb ha sido también utilizada por Faber et. al. ^[46] para inferir las energías de formación de compuestos sólidos mediante regresión Ridge utilizando Kernel ^[47]. La colección de muestras utilizada por Faber et. al. constó de 3898 sistemas sólidos que obtuvieron del sitio web Materials Project ^[48]. La construcción de los datos de entrada de las muestras de la colección se consiguió mediante tres modificaciones de la matriz de Coulomb: 1) La matriz de suma de Ewald, 2) La matriz extendida de Coulomb y 3) La matriz de seno. Los elementos de la matriz de suma de Ewald corresponden a un par de átomos en la celda primitiva. Los elementos de dicha matriz se calculan mediante la siguiente fórmula:

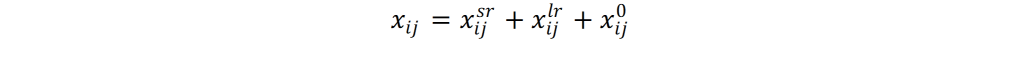
Los términos x_ij^sr y x_ij^lr corresponden a la interacción de un par de átomos i y j de corto y largo alcance, respectivamente; mientras que x_ij⁰ sirve como un término de corrección que describe la interacción de los cores atómicos. Los términos que describen la interacción en corto y largo alcance entre dos átomos i ≠ j se definen como:

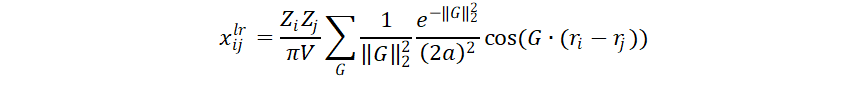
L y G  corresponden a vectores en los espacios real y recíprocos, mientras que V corresponde al volumen de la celda primitiva. Es importante la definición de un radio de corte L_max y G_max. Faber et. al. reportan que el parámetro a afecta en la velocidad de convergencia de las sumas de las interacciones de corto y largo alcance. Dicho parámetro se define como:

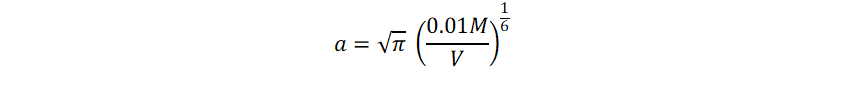
Donde M es el número de átomos en la celda primitiva.  El término correctivo se define como:

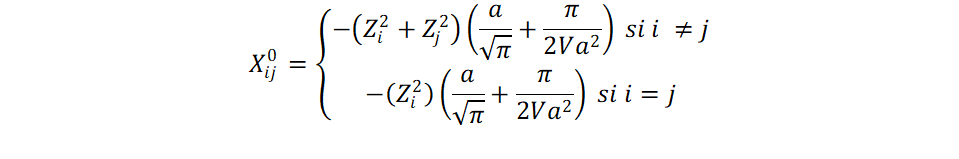
La matriz extendida de Coulomb es similar a la matriz de Coulomb original salvo que:

1) sus dimensiones son de M por MN, donde M corresponden a los átomos en la celda primitiva y N corresponde al número de celdas vecinas y;

2) El potencial utilizado tiene la forma Z_iZjexp^{||r_i – rj||}.

La matriz de seno difiere de la matriz de Coulomb original en que los elementos de matriz que no pertenecen a la diagonal se calculan como:

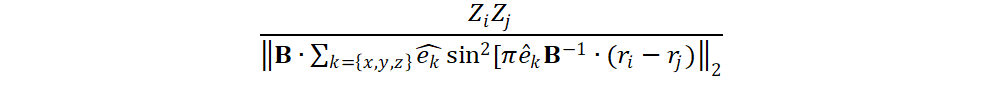
Donde B es la matriz formada por los vectores base de la celda. Los errores absolutos promedio obtenidos en por Faber et. al. fueron 0.49 eV atom^-1 con la matriz de suma de Ewald, 0.64 eV atom^-1 con la matriz extendida de Coulomb y 0.37 eV atom^-1 con la matriz de seno. Los autores sugieren que, aun cuando con la matriz de seno se hayan obtenido mejores resultados, el desempeño obtenido es prácticamente similar. Sin embargo, el cálculo de la matriz de seno es más directo que las otras dos representaciones utilizadas por Faber et. al.

Schmidt y coautores ^[49] utilizaron diferentes algoritmos de aprendizaje de máquina, entre ellos perceptrones multicapa, para determina la estabilidad termodinámica de sólidos tipo perovskita. La caracterización de las muestras que Schmidt et. al. implementaron se basó en un vector de entrada con información para cada elemento de la fórmula como el número de electrones de valencia, la electronegatividad, sus estados de oxidación más comunes, la masa atómica, el punto de fusión, entre otros. Con una colección de 249692 compuestos calculados vía DFT, y que se encuentra disponible en Materials Project, ellos obtienen un error promedio absoluto de 121 meV atom^-1 en la distancia al envolvente convexo ^[50]. Todas las muestras utilizadas poseían la estructura perovskita cúbica.

Fedorov y Shamanaev ^[51] han utilizado las redes neuronales de tipo perceptron multicapa para determinar la capacidad molar calorífica, la entropía molar estándar y la energía de red de compuestos cristalinos inorgánicos. La colección de muestras utilizadas para entrenar a las redes neuronales fue tomada de la base de datos de estructuras inorgánicas cristalinas (ICSD, por su acrónimo en inglés) y de la base de datos libre COD (Crystallography Open Database). El número de compuestos máximo utilizado en su desarrollo de redes neuronales fue de 168. La caracterización de las muestras de la colección se consigue por la caracterización de los centros topológicos ^[52] del compuesto cristalino (Thimm, 2009), para los cuales hay una red neuronal independiente. Cada centro topológico se caracteriza mediante un vector de entrada con información sobre la electronegatividad, el estado de oxidación, la masa molar, el radio covalente y la distancia entre un centro topológico y sus vecinos. Las salidas de las redes neuronales de cada centro topológico, que es un vector de una componente, son utilizadas como vector de entrada de una red neuronal que computa los valores termodinámicos mencionados. El error porcentual absoluto promedio que se consigue mediante redes neuronales y la caracterización implementada por Fedorov y Shamanaev fue menor al 8%. El trabajo desarrollado en la presente tesis es similar al publicado por Fedorov y Shamanaev, sólo que aquí se utilizaron los sitios de simetría de Wyckoff de los grupos espaciales cristalinos para definir los rasgos que caracterizan a cada compuesto.

Ye et. al ^[53]. publicaron en 2018 sobre la determinación de energías de formación de compuestos tipo granate y perovskita mediante redes neuronales de tipo perceptrón multicapa. Para el desarrollo de su algoritmo de aprendizaje de máquina utilizaron 542 compuestos tipo perovskita ABO₃ y 1407 compuestos tipo granate C₃A₂D₃O₁₂, que consistieron en compuestos puros y soluciones sólidas. La caracterización de los compuestos cristalinos implementada por Ye y coautores se basó en la caracterización de los sitios de Wyckoff de sus cationes. Los sitios de Wyckoff de los cationes fueron caracterizados mediante los radios iónicos de Shannon y las electronegatividades de Pauling promedio. A diferencia de las redes neuronales de Fedorov y Behler, en donde existe una red neuronal para cada centro topológico o átomo, todos los rasgos de los sitios de Wyckoff se concatenaron en un vector de entrada único a una red neuronal. En concreto, se obtiene un vector de entrada de seis y ocho componentes para el caso de las muestras tipo perovskita y granate, respectivamente. Ye y coautores obtuvieron un error absoluto promedio de 7 – 10 meV atom^-1 y 20 – 31 meV atom^-1 para los compuestos tipo granate y perovskita.

Javed ^[54] y Majid ^{[55 – 56]} han utilizado diversos algoritmos de aprendizaje de máquina, entre ellos las redes neuronales de tipo perceptrón multicapa, para determinar los parámetros de red de compuestos cristalinos con estructura tipo perovskita. En su colección han utilizado compuestos tipo perovskita con simetría ortorrómbica, así como con simetría monoclínica y cúbica. El error porcentual absoluto que Javed y Majid obtienen es menor al 1%. La caracterización que los autores mencionados implementaron es mediante la descripción de los radios iónicos y electronegatividades de los cationes, así como el estado de oxidación del catión más voluminoso.

Pilania y coautores ^[57-58] han utilizado máquinas de vectores soportados ^[59-60] y árboles de decisión con potenciación del gradiente ^[61] para inferir nuevos compuestos con estructura perovskita. Pilania y coautores utilizaron 185 compuestos experimentales de tipo ABX₃ ^[62] y 354 compuestos de tipo ABO₃. La caracterización de los compuestos de las colecciones usadas se consiguió a través de los radios iónicos de los elementos, el factor de tolerancia de Goldschmidt y el factor octaédrico (sección 1.2.1 de esta tesis), los radios de valencia del enlace, cocientes de suma de los radios de los orbitales s y p y diferencias de electronegatividades. Las precisiones en la clasificación global (accuracy, en inglés) fueron de 92.1 y 95.1 %.

Isayev y coautores ^[63] han caracterizado los materiales del repositorio AFLOW ^[64] mediante lo que ellos mismos han denominado como Fragmentos de materiales etiquetados con propiedades (Property-Labelled Materials Fragments, PLMF). La teselación de Voronoi ^[65] es la esencia de esta caracterización, la cual se efectúa en una partición de la estructura cristalina. Con la teselación de Voronoi se establece qué átomos están conectados. Para esto, es necesario que los átomos compartan una cara de Voronoi y que la distancia interatómica sea menor a la suma de radios covalentes de Cordero ^[66]. Mediante la teselación, se obtiene un grafo y una matriz de adyacencia, A. Los rasgos se obtienen mediante las fórmulas:

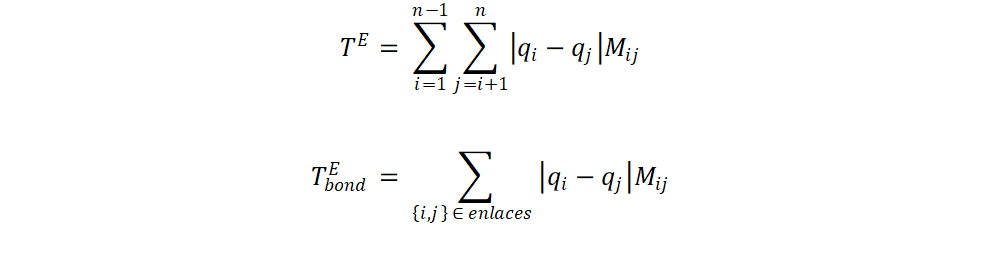
Donde M es la matriz Galvez, de dimensión nxn, donde n es el número de átomos en la celda unitaria. La matriz Galvez se obtiene del producto entre elementos de matriz A · D , donde D es la matriz recíproca de cuadrados de distancia (D_ij = 1/r_ij² ). Las variables q_i y q_j son propiedades de un átomo como el número de electrones de valencia, la masa atómica, la electronegatividad, la capacidad calorífica, la dureza química, entre otras. Con esta aproximación de Fragmentos de materiales etiquetados con propiedades se obtiene un vector de datos de entrada de 2494 rasgos, después de filtrar los rasgos con una correlación r² > 0.95 y con una varianza menor al 0.001.

Tanto Isayev y coautores como Xie y Grossman ^[67] han utilizado la caracterización por fragmentos de materiales etiquetados con propiedades para clasificar entre metales y aislantes, determinar energías absolutas, brechas energéticas, módulos de compresibilidad y corte, razones de Poisson, temperatura de Debye y capacidades caloríficas. Isayev y coautores han implementado árboles de decisión con potenciación del gradiente, mientras que Xie y Grossman utilizaron redes neuronales del tipo Convolucional. Ambos grupos utilizaron conjuntos de muestras superiores a 46,000 compuestos. Los resultados obtenidos con esta caracterización son prometedores y pueden consultarse en las referencias 63 y 67.

Referencias

41. S. Lorenz, A. Gross, M. Scheffler, Chem. Phys. Lett. 2004, 395, 210 – 215
42. J. Behler, M. Parrinello, Phys. Rev. Lett. 2007, 98, 146401
43. N. Artrith, A. Urban, Comp. Mater. Science, 2016, 114, 135 – 150
44. K. Hansen, G. Montavon, F. Biegler, S. Fazli, M. Rupp, M. Scheffler, O. A. von Lilienfeld, A. Tkatchenko, K. R. Müller, J. Chem. Theory Comput. 2013, 9, 3404 – 3419
45. M. Rupp, A. Tkatchenko, K. R. Müller, O. A. von Lilienfeld, Phys. Rev. Lett., 2012, 108, 058301
46. F. Faber, A. Lindmaa, O. A. von Lilienfeld, R. Armiento, Int. J. Quantum Chem. 2015, 115, 1094 – 1101
47. B. Schölkopf, Z. Luo, V. Vovk, Empirical Inference. Springer, 2013. ISBN: 978-3-642-41135-9
48. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder, K. A. Persson, APL Mater. 2013, 1, 011002
49. J. Schmidt, H. Shi, P. Borlido, L. Chen, S. Botti, M. A. L. Marques Chem. Mater. 2017,29, 5090 – 5103
50. a) https://mathworld.wolfram.com/ConvexHull.html (Consultado el 23 de noviembre de 2020); b) https://en.wikipedia.org/wiki/Convex_hull (Consultado el 23 de noviembre de 2020).
51. A. V. Fedorov, I. V. Shamanaev Mol. Inf. 2017, 36, 1600162
52. G. Thimm, Acta Cryst. A, 2009, 65, 213 – 226
53. W. Ye, C. Chen, Z. Wang, I. H. Chu, S. P. Ong, Nature Commun. 2018, 9, 3800
54. S. G. Javed, A. Khan, A. Majid, A. M. Mirza, J. Bashir Comput. Mater. Science, 2007, 39, 627 – 634
55. A. Majid, A. Khan, T. S. Choi, Comput. Mater. Science 2011, 50, 1879 – 1888
56. A Majid, A. Khan, G. Javed, A. M. Mirza Comput. Mater. Science 2010, 50, 363 – 372
57. G. Pilania, P. V. Balachandran, C. Kim, T. Lookman, Front. Mater. 2016, 3, 19
58. G. Pilania, P. V. Balachandran, J. E. Gubernatis, T. Lookman, Acta Cryst. B, 2015, 71, 507 – 513
59. C. Cortes, V. Vapnik, Machine Learning, 1995, 20, 273 – 297
60. W. Noble, Nat. Biotechnology, 2006, 24, 1565 – 1567
61. A. Natekin, A. Knoll, Front. Neurobot., 2013, 7, 21
62. C. Li, X. Lu, W. Ding, L. Feng, Y. Gao, Z. Guo, Acta Cryst. B, 2008, 64, 702 – 707
63. O. Isayev, C. Oses, C. Toher, E. Gossett, S. Curtarolo, A. Tropsha, Nature Comm. 2017, 8, 15679
64. S. Curtarolo, W. Setyawan, G. L. W. Hart, M. Jahnatek, R. V. Chepulskii, R. H. Taylor, S. Wang, J. Xue, K. Yang, O. Levy, M. J. Mehl, H. T. Stokes, D. O. Demchenko, D. Morgan, Comput. Mater. Science, 2012, 58, 218 – 226
65. Z. W. Salsburg, J. Chem. Educ., 1966, 43, 353 – 357
66. B. Cordero, V. Gómez, A. E. Platero-Prats, M. Revés, J. Echeverría, E. Cremades, F. Barragán, S. Alvarez, Dalton Trans., 2008, 2832 – 2838
67. T. Xie, J. C.  Grossman, Phys. Rev. Lett. 2018, 120, 145301