Symmetry-site based feature construction to characterize the crystal compounds. Part II.

Let me show you what you can find with the approach I told you in the last post.

1629 vertex-shared perovskite compounds were found in Crystallography Open Database (COD) (Figure 1). As I told you, all crystal structures (such as the perovskite structure) are defined by the occupation of certain Wyckoff sites. In the last post, I described the Wyckoff sites occupied in the ideal (aristotype) perovskite structure. The ideal perovskite structure has the space group Pm3m. A survey of the Wyckoff site occupation in the vertex-shared perovskite structure is given by P. Woodward and other authors. The perovskite structures search was based on those references.

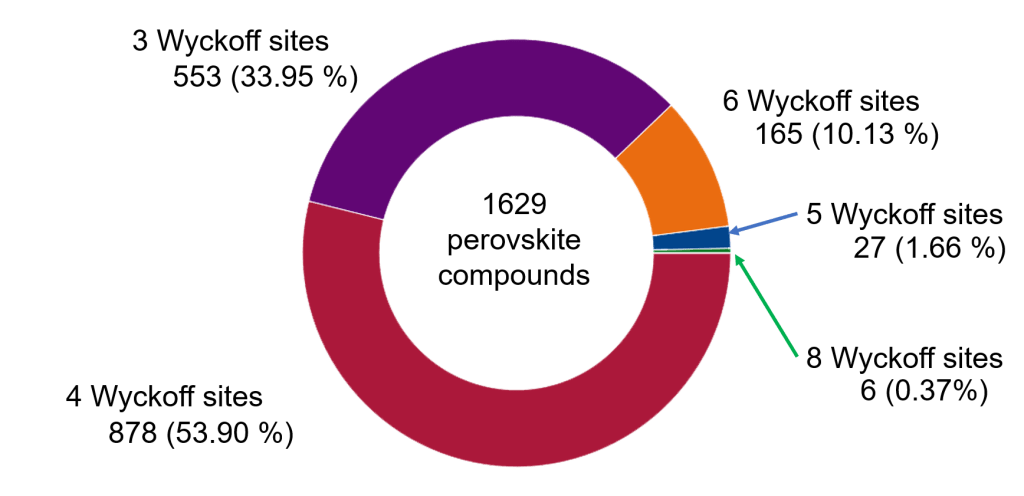
The 1629 perovskite compounds were distributed as follows: 878 (53.90 %) and 553 (33.95 %) were described by three and four Wyckoff sites. Both subsets summed up 1431 and represented 87.85 % of all the perovskites found in the database. A third subset, with 165 perovskite compounds, was described with six Wyckoff sites (10.33 %). Finally, there were two subsets, with 27 and 6 perovskite compounds, described with five and eight Wyckoff sites.

Figure 2 shows the distribution of the perovskite compounds based on their space group. The compounds having three Wyckoff sites corresponded to the space groups Pm3m (cubic) and R3c (trigonal). There were 397(24.37 % of all the found perovskite compounds) and 156 compounds in these space groups, respectively.

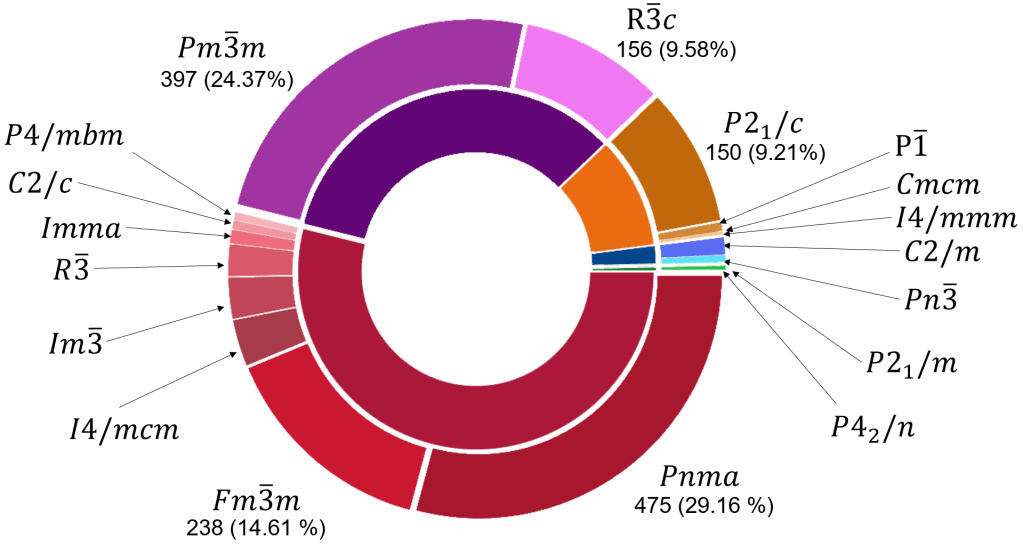
The compounds with four Wyckoff sites corresponded mainly to the space groups Pnma (orthorhombic) and Fm3m (cubic). Both space groups summed up 773 of the 878 perovskite compounds with four Wyckoff sites. It is important to mention that the compounds with the space group Fm3m were double perovskite structures, which are commonly named as elpasolites. In fact, the search of compounds having the perovskite structure spanned single and double perovskites. There were compounds with other space groups described with four Wyckoff sites: C2/m (10 compounds, monoclinic), Imma (15, orthorhombic), P4/mbm (tetragonal), I4/mcm (tetragonal), R3 (35, trigonal), and Im3 (45, cubic).

The compounds described with six Wyckoff sites corresponded mainly to the monoclinic space group P2₁/c. There were 150 of 165 compounds with this space groups. There were also 10 compounds with the space group P-1 (triclinic), 4 with the space group Cmcm (orthorhombic), and one compound in the space group I4/mmm.

The compounds described with five Wyckoff sites had the space group C2/m (19 compounds, monoclinic crystal system) and Pn3 (8, cubic). Finally, the compounds described with eight Wyckoff sites had the space groups P2₁/m (five compounds, monoclinic crystal system), and P4₂/n (one compound, tetragonal).

So far this description, you can find the perovskite compounds found in the Crystallography Open Database in this link. The perovskite compounds are among the different csv-files, either traval or test. The perovskite compounds are labeled as True in the target column. The difference of the file names, concerning to the number, is related to the number of sites used to characterize the crystal compounds. The number of sites influences the number of features (input data) you use to feed the Artificial Neural Networks. This is because the approach I use is related to the different symmetry sites in the crystal compounds. I will explain more of this in the next section.

Symmetry as a tool to reduce the crystal compound description

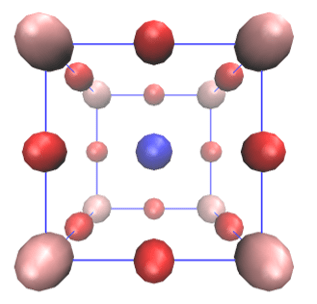
            The crystal compounds have a long-range arrangement of their particles (atoms, ions, or molecules, for example). Figure 3 shows an example of a crystal compound, which adopts the perovskite structure. This compound is BaTiO₃, barium titanium oxide. Figure 3 shows the ideal perovskite structure for BaTiO₃. In the compound, the oxygen atoms are in red, whereas the barium and titanium are colored in blue and pink, respectively. A consequence of the long-range arrangement is that it is possible to identify a minimal unit, which allows to describe the crystal by translational symmetry. The minimal unit is named as unit-cell. The existence of translational symmetry comes with the periodic nature of the crystal compounds. Furthermore, the translational symmetry allows to simplify the description of the crystal system, which has as many particles as the Avogadro constant. Then, you only need to describe the particles within the unit-cell and not all of the crystal compound.

Figure 3: BaTiO₃ crystal. The next image of the carrousel shows the unit cell of the BaTiO₃ crystal. In fact, the BaTiO₃ is generated when you repeat the unit cell four times along each coordinate axis.

            The perovskite compounds found in COD have a different number of atoms within the unit-cell. For example, in the compounds adopting the ideal perovskite structure, there are five atoms per unit-cell. The compounds adopting the perovskite structure with the space group Pnma (orthorhombic) have twenty atoms per unit-cell. The perovskite compounds with the space groups R3c have 10 atoms per unit-cell. The compounds with the elpasolite (perovskite structure with the space group Fm3m) have 40 atoms in the unit-cells. Additionally, these numbers of atoms per unit-cell correspond to the case when there are not vacancies in the structure. In such cases, you have fewer atoms or even fractional amounts of atoms, which does not mean that there are fractions of atoms in the crystal, but there are atoms absent randomly distributed over the whole crystal.

            After all, you may construct features per atom of the unit cell, but this approach will generate models suitable for a max-number of atoms in the unit cell. A question it may arise is if it is still possible to further reduce the description of the atoms in the crystal structure. The answer to this question is: Yes, it is. I will illustrate this with the examples given in the paragraph above:

• In the ideal perovskite structure, three of the five atoms of the unit-cell see the same chemical environment. The other two atoms have different chemical environments. Therefore, the atoms of the unit-cell are located in three different chemical environments. The same holds for all the atoms of the crystal (due to the periodic nature of the crystal compounds).
• The 20 atoms of the perovskite compounds with the space group Pnma are distributed over four different chemical environments.
• The 10 atoms of the perovskite compounds with the space group R3c are distributed over three different chemical environments.
• The 40 atoms of the elpasolite perovskite compounds (space group Fm3m) are distributed over four different chemical environments.

            These different chemical environments are called in crystallography as Wyckoff sites. As it was commented in the last post, the Wyckoff sites gather atoms located in positions having the same symmetry point-group. Although there are five atoms in the unit cell of the ideal perovskite structure, there are (let’s say) essentially three different kinds of atoms, due to their different chemical environments. A similar situation can be established for the ten atoms of the perovskite compounds with the space group R3c: there are three different kinds of atoms. Additionally, the perovskite compounds with the space group Pnma have basically four different kinds of atoms (again, due to their different chemical environments). Similarly, the same holds for the elpasolite compounds, where there are 40 atoms per unit-cell.

            If you really want to know more about the Wyckoff sites, I strongly recommend you to dive into chapter 8 of the International Tables of Crystallography, Volume A. I can tell you that:

• Wyckoff sites are related to symmetry point-groups.
• Those point groups are invariant subgroups of the space group of the crystal compound (in the light of the Group theory).
• The Wyckoff symbols are represented with a letter. The symmetry of the point-groups lowers alphabetically.
• The point-groups related to the symbols of the Wyckoff sites vary among the space groups.
• The number of symmetry elements present in a group is called as the order of the group. In a certain way, a group is more symmetric when it has more symmetry elements. The important thing is the following: the quotient of the order of the crystal space group with the order of the symmetry point-group associated to a Wyckoff label equals the multiplicity. This holds for crystal with a lattice of the primitive kind, P. For the crystals with a body center lattice or base center lattice, you multiply that quotient by two. For crystals with a face center lattice, you multiply the quotient by four.
• The last-mentioned ingenious quotient basically sets how many atoms can have the same chemical environment (same symmetry point-group).

            Up to now, we can say that the Wyckoff sites allows to:

• define a crystal structure.
• manage compounds with different atoms per unit-cell, as long as these compounds have the same number of Wyckoff sites.

            In the post of the following week, I will tell you how we can characterize the Wyckoff sites of a crystal compound to construct the input data of an Artificial Neural Network.

            See you then!