My Ph. D. work was about the inference of new perovskite compounds with Artificial Intelligence and quantum chemical calculations. More concretely, I used Artificial Neural Networks (ANNs) to predict compounds having the perovskite crystal structure. The ANNs I worked with were full-connected and feed-forward (also known as multilayer perceptrons). The developed ANNs classified the crystal compounds as perovskite or non-perovskite materials.
To train my ANNs, I needed a crystallographic database. It is important to mention that not all crystallographic databasis allow you to have access to their crystal information files (CIFs). Having access to CIFs is important since this will allow you to construct the input data you feed to your ANNs. Even more, CIFs are plain text files, and therefore they are easily accessed.
The primary solution to my problem was to use the Crystallography Open Database (COD). It is a database you can easily download to your computer (it can take you few hours). Once you download it, I recommend you to check that the element symbols in all CIFs are correctly written.
When I started my Ph.D., COD had a little more than 370k files. Some of the files were repeated, if you consider that two compounds are the same if they have the same formula and space group. This is a naïve approach, since you may have that two same compounds have slightly different lattice parameters (This difference can be ascribed to either the measurement or the synthesis conditions). This was not taken into account, and after deleting the repetead compounds, I ended up with around 310k files (in principle, different compounds).
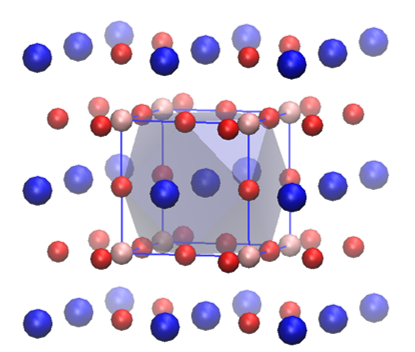
The next question it may arise is: How to find all the compounds matching the crystal structure I am looking for? The perovskite structure, with the ideal formula ABX3, consists of three diferent type of atoms: A and B are typically metals, and X is a non-metal. The A-atom is bigger than the B-atom. The A-atoms occupy sites having a cubeoctahedral geometry, which is defined by its first neighbors (X-atoms). The B-atoms occupy sites having an octahedral geometry (defined also by the first neighbors, which also are X-atoms). In fact, the main characteristic of the perovskite structure is the existence of a vertex-shared octahedral framework. The X-atoms are those located in the vertices.
Two representations of the perovskite structure. The left one shows the main characteristic of this crystal structure: the corner-shared octahedral framework. In the center of the octahedra there is an atom (not shown). The right image shows the same crystal from another perspective: It shows the cubeoctahedral voids left by the corner-shared octahedral framework.
The above description corresponds to the ideal scenario, the most symmetric form of the perovskite structure, or the aristotype of the perovskite structure. Due to relative sizes of the atoms A and B, the vertex-shared octahedral framework may distort and therefore, the search of compounds having the perovskite structure can turn a little more complicated.
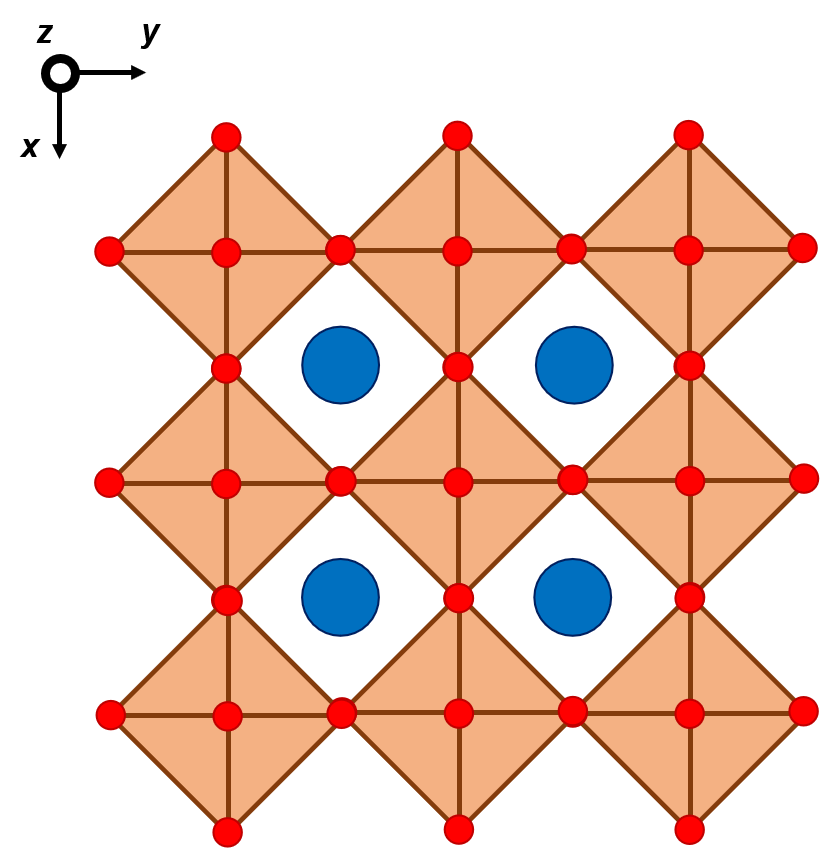

The ideal perovskite structure is sketched in the left side, as seen from above. This structure can distort if the atoms in blue are not sufficient large. In the right side you find a distorted perovskite structure. The way the perovskite structure mainly distorts is by rotation around the octahedral axes.
You can search the perovskite structures in your database one by one, perhaps with the aid of a visualization software. That will take you a lot of time and may run out all your Ph. D. scholarship! Fortunately, there is a much better way to find any crystal structure, such as the perovskite structure. This way is based on well-known principle: the atoms of a crystal structure occupy positions in real space characterized by symmetry. These positions are described with point-symmetry groups. In crystallography, the Wyckoff sites assign sets of positions having the same point-symmetry group. The Wyckoff sites consist of a coefficient and a symbol, which is a letter. The coefficient is called multiplicity and tells you the number of positions with the same point-symmetry group. The symbol is a letter and corresponds to a point-symmetry group, which vary among the 230 space groups. In addition, the order of the point-symmetry group decreases alphabetically with the label. All the information about the Wyckoff sites are in the Volume A of the International Tables of Crystallography.
There are two ways to crystallographically define the ideal perovskite structure. The ideal perovskite structure corresponds to the space group No. 221. Below you will find a fragment of the crystallographic information of this space group. One way to describe the aristotype perovskite is by the occupation of the Wyckoff sites a (cubeoctahedral atom), b (octahedral atom), and c (atoms in vertices). Another way to describe this structure is by the occupation of the Wyckoff sites a (octahedral atom), b (cubeoctahedral atom), and d (atoms in vertices). The difference in the description is related to the origin choice (you can take the origin the octahedral atom or the dodecahedral atom). Eithercase, you may notice that the ideal perovskite structure is defined by the occupation of two sites having the point-group simmetry m-3m , and one, which has the point-symmetry group 4/mmm. This approach can be also used to find the distorted perovskite structures.
| Multiplicity | Label | Point-group | Relative positions |
| 3 | d | 4/mm.m | (1/2, 0, 0); (0, 1/2, 0); (0, 0, 1/2) |
| 3 | c | 4/mm.m | (0, 1/2, 1/2); (1/2, 0, 1/2); (1/2, 1/2, 0) |
| 1 | b | m-3m | (1/2, 1/2, 1/2) |
| 1 | a | m-3m | (0, 0, 0) |
Now you know that the atoms of any crystal structure occupy specific position according to their Wyckoff sites, you can code an algorithm to find all the compounds having the crystal structure you are interested. Wait for the next post to know what comes next!